 Meine Feiertags- und Neujahrskarte enthält einige zufällig dargestellte Sterne – das Ergebnis einer Geometrie-Spielerei. Nachtrag 2. Januar 2023: Es gibt zusätzlich eine digitale Neujahrskarte mit 23 farbigen 23-zackigen Sternen und sternförmigen Polygonen.
Meine Feiertags- und Neujahrskarte enthält einige zufällig dargestellte Sterne – das Ergebnis einer Geometrie-Spielerei. Nachtrag 2. Januar 2023: Es gibt zusätzlich eine digitale Neujahrskarte mit 23 farbigen 23-zackigen Sternen und sternförmigen Polygonen.
Sterne? Das sind doch die Zentralgestirne von Planeten-Systemen. Nun, nicht nur in der Feiertagszeit sind Sterne eine beliebte Dekoration. Auch als Markensymbole und Wappeninhalte haben Sterne in unterschiedlichen Formen eine beachtliche Bedeutung.
Gezeichnete Sterne
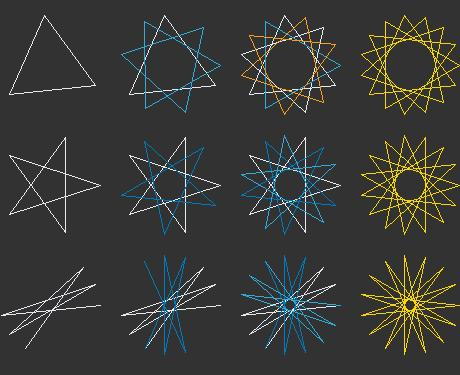
Diese Sterne sind gezackt, so ab drei Zacken aufwärts. Hier mal eine Sammlung in je vier Varianten von fünf- bis sechzehn-zackig:

Im Sinne der klassischen Definition gelten nur die Sterne der dritten Zeile – als Strichkonstruktion – als «echte» Sterne. Die Sterne in der zweiten Zeile kommen, wenn auch mit Farbe gefüllt, diesen «echten» Sternen am nächsten.
- Der Fünfstern wird auch als Pentagramm bezeichnet. Dieser Stern wird mittels Sehnen als Verbindung von fünf gleichmässig auf einem Kreis verteilten Punkten konstruiert.
- Als Hexagramm wird ein Stern mit sechs Zacken bezeichnet. Konstruktion auch hier mit sechs gleichmässig über einen Kreisumfang verteilten Punkten – zu zwei gleichseitigen Dreiecken verbunden.
- Mit sieben Zacken folgt das Heptagramm. Auch wieder sieben gleichmässig um einen Kreis verteilte Punkte. Und da gibt es bereits Konstruktionsvarianten: entweder wird jeweils von einem Punkt aus mit dem übernächste Punkt verbunden oder sogar der über-übernächste Punkt, also wie die Strichkonstuktion dritte Zeile von oben, dritter Stern von links.
- Das Oktagramm kann aus zwei um 45 Winkelgrade verschobenen Quadraten konstruiert werden. Auch hier können acht gleichmässig um einen Kreis verteilte Punkte verbunden werden, jeweils mit dem über-übernächsten Punkt.
- Der neunzackige Stern besteht entweder wie oben dritte Zeile, fünfter Stern von links aus drei jeweils um 40 Winkelgrade verschobene gleichseitige Dreiecken. Oder auch hier funktioniert die Konstruktion über gleichmässig über einen Kreis verschobene Punkte.
- Der zehnzackige Stern lässt sich aus zwei Pentagrammen zusammensetzen. Für den fünfzehn-zackigen Stern braucht es demnach drei Pentagramme.
- Auch der elfzackige und der dreizehn-zackige Stern orientieren sich an den gleichmässig um den Kreis verteilten Punkten.
- Der zwölfzackige und der fünfzehn-zackige Stern können aus vier respektive fünf gleichseitigen Dreiecken konstuiert werden.
- Der zwölfzackige Stern lässt sich auch aus drei Vierecken zeichnen – für den sechzehn-zackigen Stern braucht es vier Vierecke.
- Der vierzehn-zackige Stern wiederum besteht aus zwei Heptagrammen.
Illustration der Fünfzehn-Zacken-Varianten
Bei zahlreichen Zacken gibt es mehrere Varianten zur Darstellung der Sterne, hier am Beispiel des Fünfzehn-Zackers. Gezeichnet mit fünf Dreiecken, dann drei Fünfecken/Pentagrammen, und als ein Fünfzehn-Zacker, von links nach rechts der Aufbau, am rechten Rand zur Wiederholung in einheitlicher Farbe. Selbst ein Illustrations-Stern kann unterschiedlich konstruiert werden, mit verschiedenen Erscheinungsformen, immer aber mit gleich vielen Zacken.
Spielen mit Geometrie
Die ausgefüllten Gebilde gelten aus geometrischer Sicht nicht zwingend als Sterne, ausser sie entsprechen der Vorgabe, dass alle Kanten jeweils als eine Kreissehne entstanden aus der Verbindung von zwei der um den Kreis gleichmässig verteilten Zackenpunkte entstehen. Alle anderen Formen sind als als konkave und/oder überschlagene Polygone zu bezeichen. Das als elfzackiger Stern wahrgenommene Gebilde ist geometrisch betrachtet ein zweiundzwanzig-eckiges konkaves Polygon.
Der siebenzackige Stern ist somit als regelmässig überschlagenes Polygon zu bezeichen, zumindest in der Darstellung zweite Zeile von oben, dritter Stern von links.
Ich habe diese Sterne, die konkaven und/oder überschlagenen Polygone mit den bildgebenden Funktionen der PHP-Skriptsprache zeichnen lassen. Das «Bild» wird dadurch zum geometrischen Zeichenbrett mit X-Y-Koordinaten. Für die Berechungen der Zackenpunkte der Sterne oder der Ecken der Polygone braucht es daher auch Cosinus- und Sinusfunktionen. Dies ist die Erklärung für den Titel «Geometrie»-Spielereien.
Für die Darstellung auf der Grusskarte habe ich Zufallsfunktionen verwendet. Es ist für mich offen, ob regelmässige Zackensterne oder Polygone besser aussehen als zufällig leicht «verzerrte» Gebilde.
